Matrix Inversion Using Fixed-Point Arithmetic
Matrix Inversion Using Fixed-Point Arithmetic
Matrix Inversion Using Fixed-Point Arithmetic


Overview
As part of the SENG 440 course, my team and I developed an optimized matrix inversion algorithm using fixed-point arithmetic tailored for embedded systems. Our objective was to implement matrix inversion for an 11x11 matrix on an ARM-based virtual machine, focusing on computational efficiency, precision, and suitability for embedded platforms where floating-point operations are costly.
Technical Approach
System Components:
Processor: ARM Virtual Machine for testing and optimization.
Algorithm: Gauss-Jordan elimination with pivoting.
Arithmetic: Fixed-point arithmetic to enhance performance and precision.
Optimizations: Various software-level enhancements to improve computational efficiency on embedded systems.
Development Process:
Background and Planning: We began by understanding the importance of matrix inversion in embedded systems, particularly for applications requiring efficient numerical computations. We planned to implement the Gauss-Jordan elimination method using fixed-point arithmetic on an ARM-based platform.
Initial Implementation: The initial code implemented the Gauss-Jordan elimination algorithm to invert an 11x11 matrix, serving as the baseline for subsequent optimizations.
Optimizations: We applied several optimizations specifically targeting the constraints of embedded systems:
Scaling Factor: Used a power-of-2 scaling factor to simplify multiplication and division operations into bit shifts, reducing computational complexity.
Variable Types: Employed 16-bit short integers to reduce memory usage and enhance cache efficiency, using 32-bit integers for intermediate computations to prevent overflow.
Operator Strength Reduction: Replaced expensive operations like division with more efficient bit shifts.
Pivoting and Cache Misses: Introduced row indexing to optimize cache usage during pivoting operations.
Register Usage: Utilized the
registerkeyword to suggest frequently accessed variables be stored in CPU registers.Vectorization with NEON Intrinsics: Leveraged ARM's NEON SIMD architecture for parallel processing of matrix elements.
Additional Optimizations: Implemented loop unrolling, constant propagation, and software pipelining to minimize loop overhead and improve execution speed.
Challenges and Solutions
Precision and Performance:
Challenge: Balancing precision and performance in matrix inversion, critical for embedded systems with limited resources.
Solution: Used fixed-point arithmetic with an appropriate scaling factor to retain precision while enhancing computational efficiency.
Cache Efficiency:
Challenge: Optimizing cache usage during matrix operations, crucial for embedded systems with limited memory.
Solution: Introduced row indexing to reduce cache misses and improve memory access patterns.
Vectorization:
Challenge: Efficiently parallelizing matrix operations to leverage embedded system capabilities.
Solution: Employed NEON intrinsics to perform concurrent processing of multiple data elements, significantly speeding up matrix operations.
Project Outcomes
Current Functionality:
The optimized code successfully inverts an 11x11 matrix with enhanced performance and precision suitable for embedded systems.
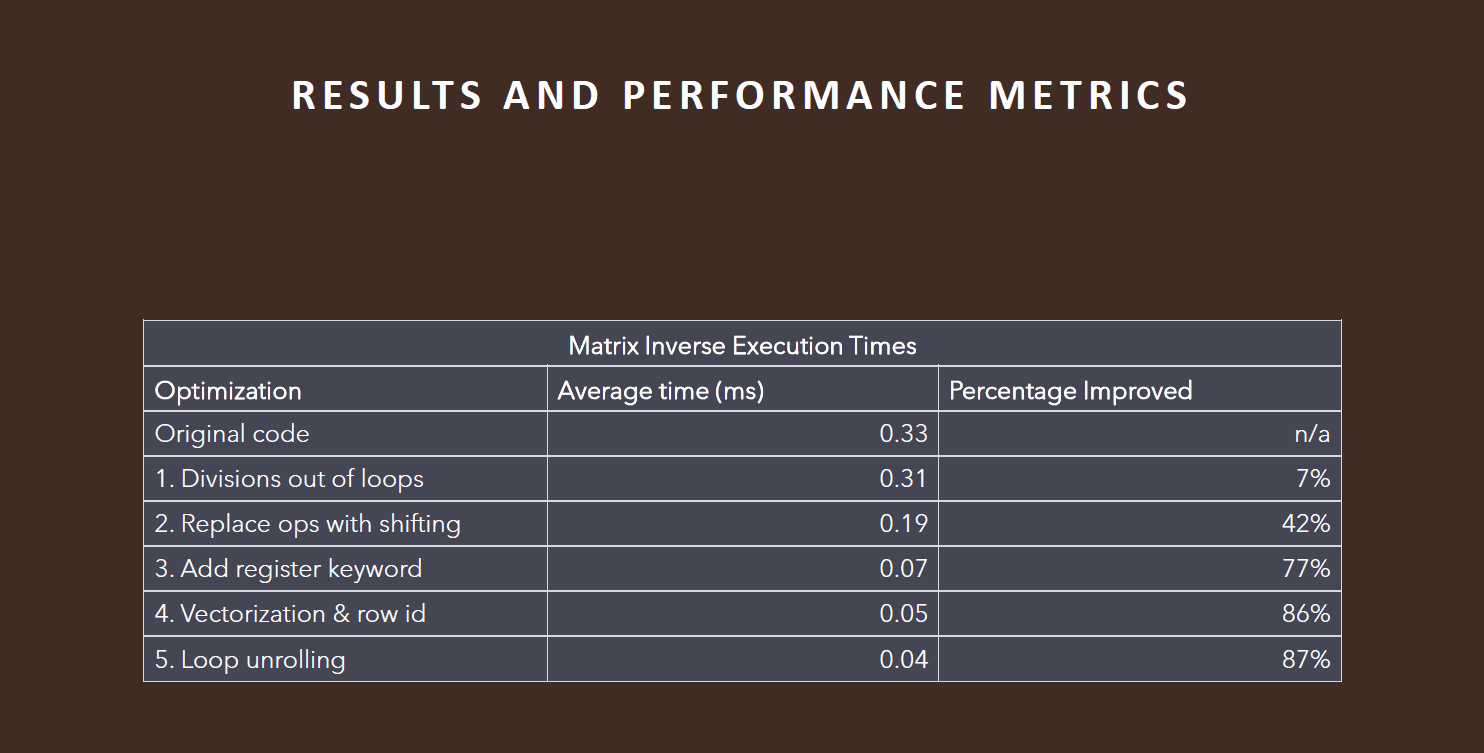
Execution times were significantly improved through various optimizations, with a final time improvement of 83% over the original code.
Performance Metrics:
Execution times for matrix inversion and condition number estimation were reduced by up to 87%, demonstrating the effectiveness of the optimizations.
Limitations:
The code's performance is highly dependent on the condition number of the input matrix. Matrices with higher condition numbers may still pose challenges in terms of accuracy and stability.
Future Improvements
Enhanced Algorithms: Exploring more advanced algorithms for matrix inversion to further improve performance and stability on embedded platforms.
Extended Bit-width: Utilizing higher bit-width integers for better precision in fixed-point arithmetic.
Hardware Implementation: Implementing the optimized code on actual ARM hardware to validate performance gains in a real-world embedded system setting.
Conclusion
The Matrix Inversion Using Fixed-Point Arithmetic project showcased the importance of software-level optimizations in numerical methods for embedded systems. By combining fixed-point arithmetic with various optimization techniques, we achieved significant performance improvements, paving the way for efficient numerical computations on resource-constrained platforms.
Overview
As part of the SENG 440 course, my team and I developed an optimized matrix inversion algorithm using fixed-point arithmetic tailored for embedded systems. Our objective was to implement matrix inversion for an 11x11 matrix on an ARM-based virtual machine, focusing on computational efficiency, precision, and suitability for embedded platforms where floating-point operations are costly.
Technical Approach
System Components:
Processor: ARM Virtual Machine for testing and optimization.
Algorithm: Gauss-Jordan elimination with pivoting.
Arithmetic: Fixed-point arithmetic to enhance performance and precision.
Optimizations: Various software-level enhancements to improve computational efficiency on embedded systems.
Development Process:
Background and Planning: We began by understanding the importance of matrix inversion in embedded systems, particularly for applications requiring efficient numerical computations. We planned to implement the Gauss-Jordan elimination method using fixed-point arithmetic on an ARM-based platform.
Initial Implementation: The initial code implemented the Gauss-Jordan elimination algorithm to invert an 11x11 matrix, serving as the baseline for subsequent optimizations.
Optimizations: We applied several optimizations specifically targeting the constraints of embedded systems:
Scaling Factor: Used a power-of-2 scaling factor to simplify multiplication and division operations into bit shifts, reducing computational complexity.
Variable Types: Employed 16-bit short integers to reduce memory usage and enhance cache efficiency, using 32-bit integers for intermediate computations to prevent overflow.
Operator Strength Reduction: Replaced expensive operations like division with more efficient bit shifts.
Pivoting and Cache Misses: Introduced row indexing to optimize cache usage during pivoting operations.
Register Usage: Utilized the
registerkeyword to suggest frequently accessed variables be stored in CPU registers.Vectorization with NEON Intrinsics: Leveraged ARM's NEON SIMD architecture for parallel processing of matrix elements.
Additional Optimizations: Implemented loop unrolling, constant propagation, and software pipelining to minimize loop overhead and improve execution speed.
Challenges and Solutions
Precision and Performance:
Challenge: Balancing precision and performance in matrix inversion, critical for embedded systems with limited resources.
Solution: Used fixed-point arithmetic with an appropriate scaling factor to retain precision while enhancing computational efficiency.
Cache Efficiency:
Challenge: Optimizing cache usage during matrix operations, crucial for embedded systems with limited memory.
Solution: Introduced row indexing to reduce cache misses and improve memory access patterns.
Vectorization:
Challenge: Efficiently parallelizing matrix operations to leverage embedded system capabilities.
Solution: Employed NEON intrinsics to perform concurrent processing of multiple data elements, significantly speeding up matrix operations.
Project Outcomes
Current Functionality:
The optimized code successfully inverts an 11x11 matrix with enhanced performance and precision suitable for embedded systems.
Execution times were significantly improved through various optimizations, with a final time improvement of 83% over the original code.
Performance Metrics:
Execution times for matrix inversion and condition number estimation were reduced by up to 87%, demonstrating the effectiveness of the optimizations.
Limitations:
The code's performance is highly dependent on the condition number of the input matrix. Matrices with higher condition numbers may still pose challenges in terms of accuracy and stability.
Future Improvements
Enhanced Algorithms: Exploring more advanced algorithms for matrix inversion to further improve performance and stability on embedded platforms.
Extended Bit-width: Utilizing higher bit-width integers for better precision in fixed-point arithmetic.
Hardware Implementation: Implementing the optimized code on actual ARM hardware to validate performance gains in a real-world embedded system setting.
Conclusion
The Matrix Inversion Using Fixed-Point Arithmetic project showcased the importance of software-level optimizations in numerical methods for embedded systems. By combining fixed-point arithmetic with various optimization techniques, we achieved significant performance improvements, paving the way for efficient numerical computations on resource-constrained platforms.
Overview
As part of the SENG 440 course, my team and I developed an optimized matrix inversion algorithm using fixed-point arithmetic tailored for embedded systems. Our objective was to implement matrix inversion for an 11x11 matrix on an ARM-based virtual machine, focusing on computational efficiency, precision, and suitability for embedded platforms where floating-point operations are costly.
Technical Approach
System Components:
Processor: ARM Virtual Machine for testing and optimization.
Algorithm: Gauss-Jordan elimination with pivoting.
Arithmetic: Fixed-point arithmetic to enhance performance and precision.
Optimizations: Various software-level enhancements to improve computational efficiency on embedded systems.
Development Process:
Background and Planning: We began by understanding the importance of matrix inversion in embedded systems, particularly for applications requiring efficient numerical computations. We planned to implement the Gauss-Jordan elimination method using fixed-point arithmetic on an ARM-based platform.
Initial Implementation: The initial code implemented the Gauss-Jordan elimination algorithm to invert an 11x11 matrix, serving as the baseline for subsequent optimizations.
Optimizations: We applied several optimizations specifically targeting the constraints of embedded systems:
Scaling Factor: Used a power-of-2 scaling factor to simplify multiplication and division operations into bit shifts, reducing computational complexity.
Variable Types: Employed 16-bit short integers to reduce memory usage and enhance cache efficiency, using 32-bit integers for intermediate computations to prevent overflow.
Operator Strength Reduction: Replaced expensive operations like division with more efficient bit shifts.
Pivoting and Cache Misses: Introduced row indexing to optimize cache usage during pivoting operations.
Register Usage: Utilized the
registerkeyword to suggest frequently accessed variables be stored in CPU registers.Vectorization with NEON Intrinsics: Leveraged ARM's NEON SIMD architecture for parallel processing of matrix elements.
Additional Optimizations: Implemented loop unrolling, constant propagation, and software pipelining to minimize loop overhead and improve execution speed.
Challenges and Solutions
Precision and Performance:
Challenge: Balancing precision and performance in matrix inversion, critical for embedded systems with limited resources.
Solution: Used fixed-point arithmetic with an appropriate scaling factor to retain precision while enhancing computational efficiency.
Cache Efficiency:
Challenge: Optimizing cache usage during matrix operations, crucial for embedded systems with limited memory.
Solution: Introduced row indexing to reduce cache misses and improve memory access patterns.
Vectorization:
Challenge: Efficiently parallelizing matrix operations to leverage embedded system capabilities.
Solution: Employed NEON intrinsics to perform concurrent processing of multiple data elements, significantly speeding up matrix operations.
Project Outcomes
Current Functionality:
The optimized code successfully inverts an 11x11 matrix with enhanced performance and precision suitable for embedded systems.
Execution times were significantly improved through various optimizations, with a final time improvement of 83% over the original code.
Performance Metrics:
Execution times for matrix inversion and condition number estimation were reduced by up to 87%, demonstrating the effectiveness of the optimizations.
Limitations:
The code's performance is highly dependent on the condition number of the input matrix. Matrices with higher condition numbers may still pose challenges in terms of accuracy and stability.
Future Improvements
Enhanced Algorithms: Exploring more advanced algorithms for matrix inversion to further improve performance and stability on embedded platforms.
Extended Bit-width: Utilizing higher bit-width integers for better precision in fixed-point arithmetic.
Hardware Implementation: Implementing the optimized code on actual ARM hardware to validate performance gains in a real-world embedded system setting.
Conclusion
The Matrix Inversion Using Fixed-Point Arithmetic project showcased the importance of software-level optimizations in numerical methods for embedded systems. By combining fixed-point arithmetic with various optimization techniques, we achieved significant performance improvements, paving the way for efficient numerical computations on resource-constrained platforms.

